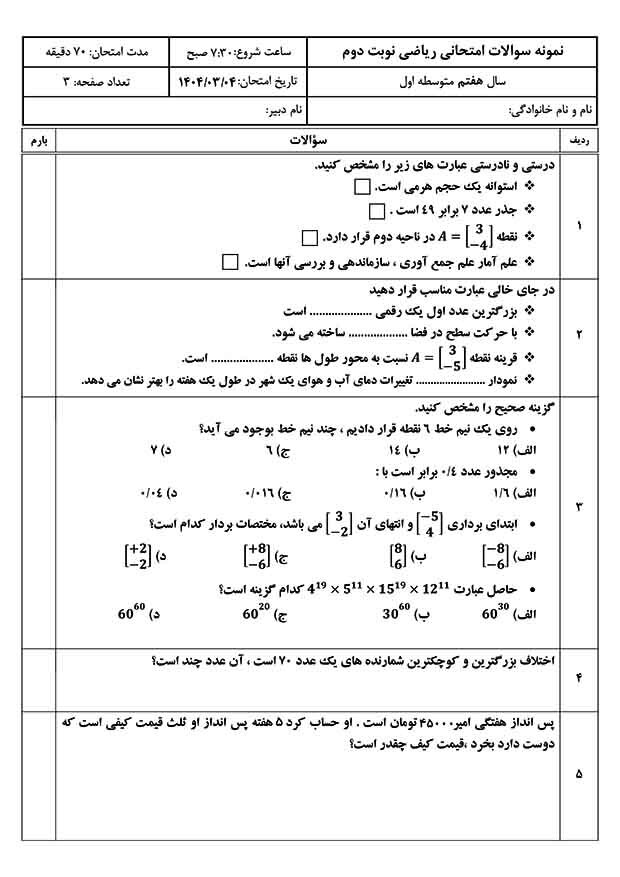
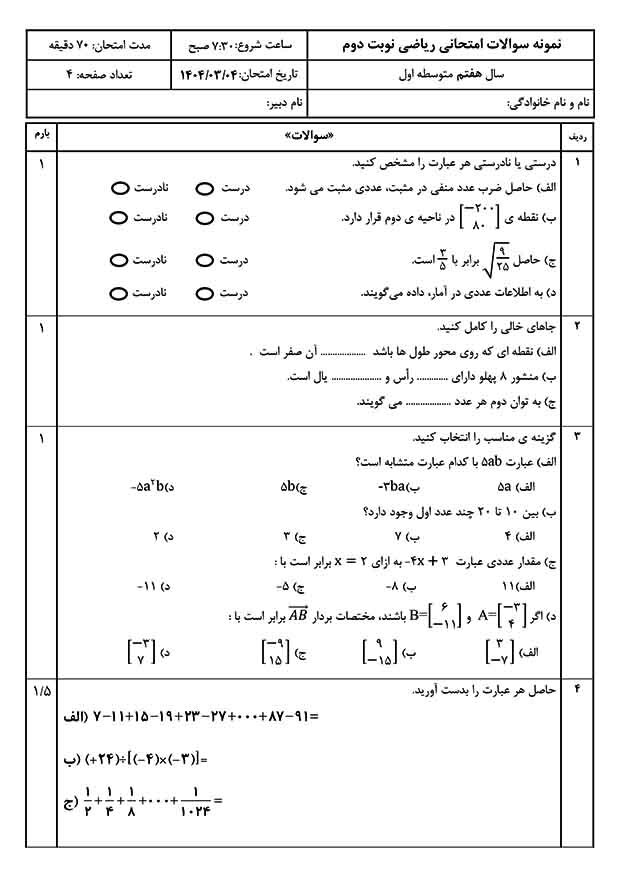
حدس کولاتز (Collatz Conjecture) که به نام "مسئله ۳n+1" هم شناخته میشود، یکی از معروفترین و سادهترین مسائل حلنشده ریاضی است. در ظاهر بسیار ساده به نظر میرسد، اما از دهه ۱۹۳۰ تا امروز ذهن ریاضیدانان را به چالش کشیده است!
حدس کولاتز به زبان ساده:
۱. یک عدد صحیح مثبت انتخاب کن (مثلاً عدد ۶).
۲. دو قانون ساده را دنبال کن:
- اگر عدد زوج است: آن را تقسیم بر ۲ کن. (n → n/2)
- اگر عدد فرد است: آن را ضرب در ۳ کن و بعلاوه ۱ بگذار. (n → 3n + 1)
۳. این مراحل را با عدد جدید تکرار کن.
۴. حدس میگوید: "همیشه" به عدد ۱ خواهی رسید! (و سپس در یک چرخه ۴ → ۲ → ۱ گیر میکنی).
مثال با عدد ۶:
۶ (زوج) → ۶ ÷ ۲ = ۳
۳ (فرد) → ۳ × ۳ + ۱ = ۱۰
۱۰ (زوج) → ۱۰ ÷ ۲ = ۵
۵ (فرد) → ۵ × ۳ + ۱ = ۱۶
۱۶ (زوج) → ۱۶ ÷ ۲ = ۸
۸ (زوج) → ۸ ÷ ۲ = ۴
۴ (زوج) → ۴ ÷ ۲ = ۲
۲ (زوج) → ۲ ÷ ۲ = ۱
نتیجه: پس از ۸ مرحله به ۱ رسیدیم!
چرا این حدس جنجالی است؟
- برای همه اعداد امتحان شده است: کامپیوترها این حدس را برای تمام اعداد تا ۲⁶⁸ (≈ ۳۰۰ کوینتیلیون!) بررسی کردهاند و همیشه به ۱ رسیدهاند.
- اما هیچ اثبات ریاضی وجود ندارد: آیا واقعاً برای هر عدد طبیعی این اتفاق میافتد؟ هیچکس نمیداند!
- پیچیدگی غیرمنتظره: دنبالههای تولیدشده گاهی بالا و پایینهای عجیبی دارند. مثلاً برای عدد ۲۷:
- ۲۷ → ۸۲ → ۴۱ → ۱۲۴ → ... → مرحله ۱۱۱ام به ۱ میرسد!
- اوج دنباله: به ۹۲۳۲ میرسد!
معمای اصلی:
- آیا ممکن است عددی وجود داشته باشد که هرگز به ۱ نرسد؟ مثلاً:
- به چرخهای تناوبی غیر از ۴ → ۲ → ۱ وارد شود؟
- یا تا بینهایت بزرگ شود؟
اهمیت حدس کولاتز:
- این حدس ارتباط عمیقی با نظریه اعداد، دینامیک و نظریه ارگودیک دارد.
- اگر اثبات شود، میتواند به درک ساختار اعداد و رفتار سیستمهای پویا کمک کند.
- نشاندهنده این است که مسائل به ظاهر ساده ممکن است عمق شگفتانگیزی داشته باشند!
پل اردش (ریاضیدان مشهور) در این باره میگوید:
"ریاضیات هنوز برای حل چنین مسئلهای نابالغ است!"