هندسه در اصل، علم اندازهگیری زمین بوده است.
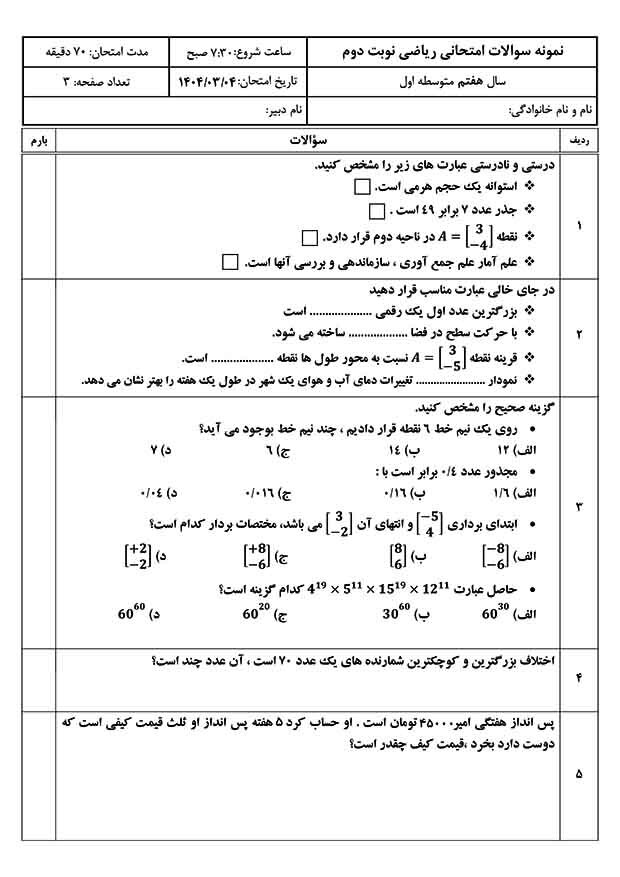
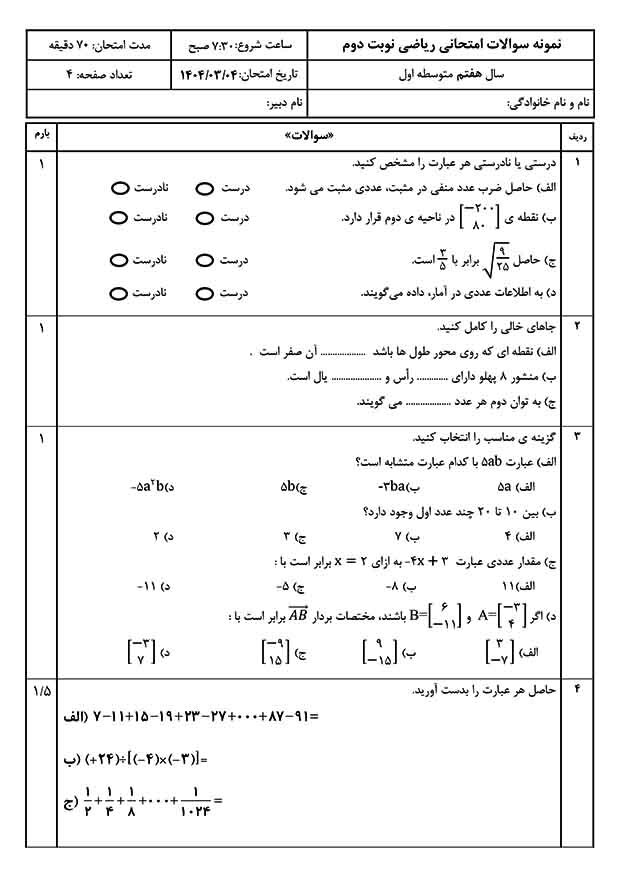
هرودت پیدایش هندسه را به مساحان مصری نسبت میدهد، ولی تمدنهای دیگر مانند بابلی، هندی و چینی نیز اطلاعات بسیاری داشتهاند.
هندسه پیشینیان در واقع گردآوردهای بود که از راه آزمایش، بررسی شباهتها، حدسها و شهودهای اتفاقی به دست میآمد.
در واقع هندسه موضوعی تجربی بود که جوابهای تقریبی آن معمولاً برای مقاصد عملی کافی بود.
بابلیها ۱۶۰۰ تا ۲۰۰۰ سال پیش از میلاد مسیح، محیط دایره را ۳ برابر قطرش میگرفتند.
حدسهای مصریان در پارهای از موارد درست و در موارد دیگر نادرست بودند. یکی از کارهای برجسته آنان یافتن دستور صحیح برای حجم هرم ناقصِ مربعالقاعده بوده است.
هندسه مصری به معنی یونانی کلمه علم نبود، بلکه صرفاً انباری از قواعد محاسبه، بیهیچ توجیهی بود.
بابلیان در حساب و جبر بسیار پیشرفتهتر از مصریان بودند. آنان بسیار قبل از تولد فیثاغورس، قضیه فیثاغورس را میدانستند.
یونانیان، و پیش از همه تالس، اصرار داشتند که احکام هندسی باید از راه استدلال قیاسی ثابت شوند نه از راه آزمایش و خطا.
تالس نخستین هندسه منطقی را بنیاد نهاد. نظامبخشی و تابع اصولسازی پس از او به مدت دو قرن توسط فیثاغورس و شاگردانش ادامه یافت.
زمانی که فیثاغورسیان طولهای گنگ، مانند رادیکال ۲ را کشف کردند، به سختی یکه خوردند و در آغاز کوشیدند که این کشف را پوشیده نگاه دارند.
مردی که نخستین بار نگره اعداد گنگ را آشکار کرد، هنگام غرق یک کشتی از میان رفت تا چیزی که بیانناشدنی و تصورناپذیر است برای همیشه پوشیده بماند.
از آنجایی که فیثاغورسیان رادیکال ۲ را عدد نمیشمردند، جبر خود را به صورت هندسی درآوردند تا بتوانند طولهای گنگ را به صورت پارهخط نشان دهند.
گرچه آنها هیچگاه نتوانستند نگره تناسبهایی را که بر طولهای گنگ نیز جاری باشد بسط دهند.
روش سقراطی محاوره اصولاً روش اثبات نامستقیم است که با آن نشان داده میشود که حکم زمانی نادرست است که به تناقضی منجر شود.
افلاطون کراراً اثبات گنگ بودن طول قطر مربعی به اضلاع واحد را به عنوان مثالی برای یک روش اثبات نامستقیم (برهان خلف) آورده است.
نکته اینجاست که این گنگ بودن طول هرگز نتوانسته از راه اندازهگیریهای عینی، که همیشه متضمن یک حاشیه کوچک تجربی خطاست، کشف شود.
اقلیدس کتابی با موضوع نگره اعداد و هندسه یونانی را در اصول سیزده جلدیش منتشر کرد که چنان جانشین کوششهای پیشین در شناسانیدن هندسه شد که کمتر نشانهای از آن کوششها به جا ماند.
اقلیدس تنها مؤلفی است که اثرش بیش از هر کسی در تاریخ بشریت خوانده شده است.
روش او در هندسه بیش از ۲۰۰۰ سال بر آموزش این ماده مؤثر بود.
بعلاوه، روشی که برای اثبات درستی نتایج (روش بنداشتی) به کار برد، الگویی است برای آنچه که امروز ریاضیات محض خوانده میشود.
هیچ تجربه عینی برای تحقیق درستی احکام لازم نیست، فقط باید مراقب استدلال در اثبات قضایا بود.
اصول اقلیدس از این جنبه نیز محض است که متضمن هیچ کاربرد عملی نیست.
گرچه کاربردهای بسیاری در مسائل عملی مهندسی داشته، ولی در اصول اشارهای به آنها نشده است.
در افسانه آمده است که روزی یکی از آموزندگان مبتدی هندسه از اقلیدس پرسید: از آموختن این مطالب چه عاید من میشود؟
اقلیدس غلامش را خواند و گفت: سکهای به او بده، چون میخواهد از آنچه فرا میگیرد چیزی عایدش شود.
این گونه تلقی از کاربرد ریاضیات در میان بسیاری از ریاضیدانان محض تا به امروز متداول مانده است.
آنها ریاضیات را صرفاً برای خودش و برای زیبایی و ظرافت ذاتیاش فرا میگیرند.
گرچه جای شگفتی است که ریاضیات محض اغلب کاربردهایی پیدا میکند که خالق آن هرگز خوابش را هم نمیدیده است.
منابع:
- Boyer, Carl B. A History of Mathematics. John Wiley & Sons, 1991.
- Burton, David M. The History of Mathematics: An Introduction. McGraw-Hill Education, 2010.
- History of Geometry – Wikipedia
- Euclid – Wikipedia
- Ancient Egyptian Mathematics – Wikipedia
- Babylonian Mathematics – Wikipedia
- The Elements by Euclid – Project Gutenberg
- Droyster, David – Class Notes, University of Kentucky
- Mathnasium: A Brief History of Geometry
- The Geodes: History of Geometry