کاربست تجزیه و اتحاد (قسمت دوم)

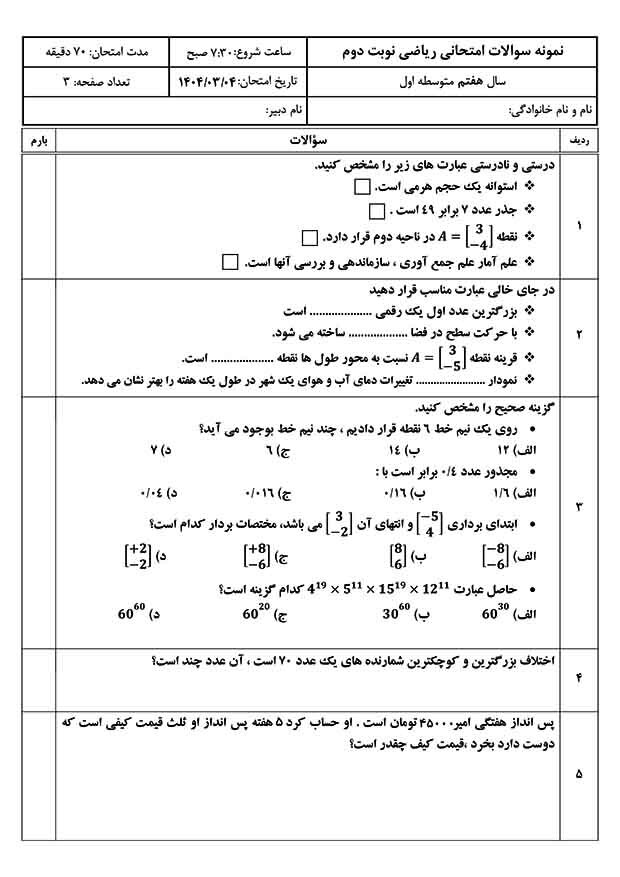
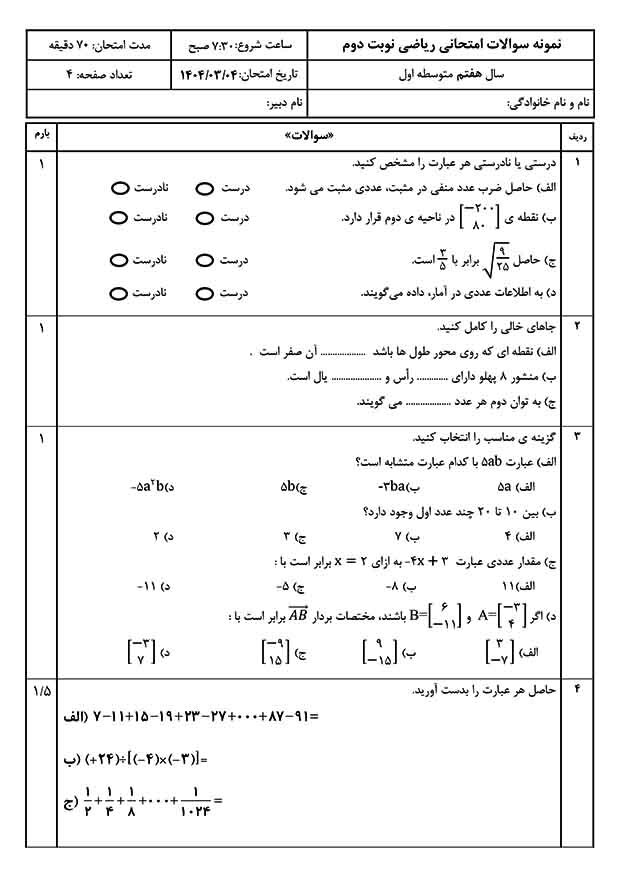
ترفند مجذور کردن سریع عددهای 41 تا 49:

برای به‌دست آوردن مجذور عددهایی مثل ۴۳، ۴۶ یا ۴۹، می‌توانیم از اتحاد مربع دو جمله‌ای به صورت هوشمندانه استفاده کنیم. فرض کنیم عدد مورد نظر ما، ۴۰ به‌علاوه‌ی عددی تک‌رقمی باشد مثلاً  40 + m:

$$(40 + m)^2 = (50 - 10 + m)^2 = (50 - (10 - m))^2$$

$$ = 50^2 - 2 \times 50 \times (10 - m) + (10 - m)^2$$

$$ = 2500 - 100 (10 - m) + (10 - m)^2$$

$$ = 2500 - 1000 + 100m + (10-m)^2$$

$$ = 1500 + 100m + (10-m)^2$$

$$ = 100 \times (15+m) + (10-m)^2$$

در واقع برای مجذور کردن اعداد 41 تا 49، کافیست مراحل زیر را دنبال کنیم:
1) یکان را با عدد 15 جمع کرده و حاصل را در 100 ضرب کنیم.
2) یکان را از عدد 10 کم کرده و حاصل را مجذور کنیم.
3) حاصل مراحل 1 و 2 را با هم جمع کنیم.

برای مثال: مجذور عدد 47 را به دست آورید.
راه حل: 

$$ 47^2 = (40 + 7)^2 = 100 \times (15+7) + (10-7)^2$$

$$ = 2200 + 9 = 2209$$

مثال‌های تمرینی:

• ذهنی حاسبه کن: \(44 × 44\)
• ذهنی محاسبه کن: \(41 × 41\)
• ذهنی محاسبه کن: \(49 × 49\)

ترفند مجذور کردن سریع عددهای ۵۱ تا ۵۹:

برای به‌دست آوردن مجذور عددهایی مثل 5۶ می‌توانیم از اتحاد مربع دو جمله‌ای به صورت هوشمندانه استفاده کنیم. فرض کنیم عدد مورد نظر ما، 50 به‌علاوه‌ی عددی تک‌رقمی باشد مثلاً  50 + m:

$$(50+m)^2 = 50^2+2 \times 50 \times m + m^2$$

$$ = 2500 + 100 m + m^2$$

$$ = 100(25+m) + m^2$$

در واقع برای مجذور کردن اعداد 51 تا 59، کافیست مراحل زیر را دنبال کنیم:
1) یکان را با عدد 25 جمع کرده و حاصل را در 100 ضرب کنیم.
2) مجذور یکان را به دست می‌آوریم.
3) حاصل مراحل 1 و 2 را با هم جمع کنیم.

برای مثال: مجذور عدد 54 را به دست آورید.
راه حل: 

$$ 54^2 = (50 + 4)^2 = 100 \times (25+4) + (4)^2$$

$$ = 2900 + 16 = 2916$$

مثال‌های تمرینی:

• ذهنی حاسبه کن: \(52 × 52\)
• ذهنی محاسبه کن: \(57 × 57\)
• ذهنی محاسبه کن: \(58 × 58\)

مثال‌های تمرینی:

• ذهنی محاسبه کن: \(53 × 52\)
• ذهنی محاسبه کن: \(57 × 56\)
• ذهنی محاسبه کن: \(48 × 49\)

منبع:
کتاب «در پی فیثاغورث»، از پرویز شهریاری