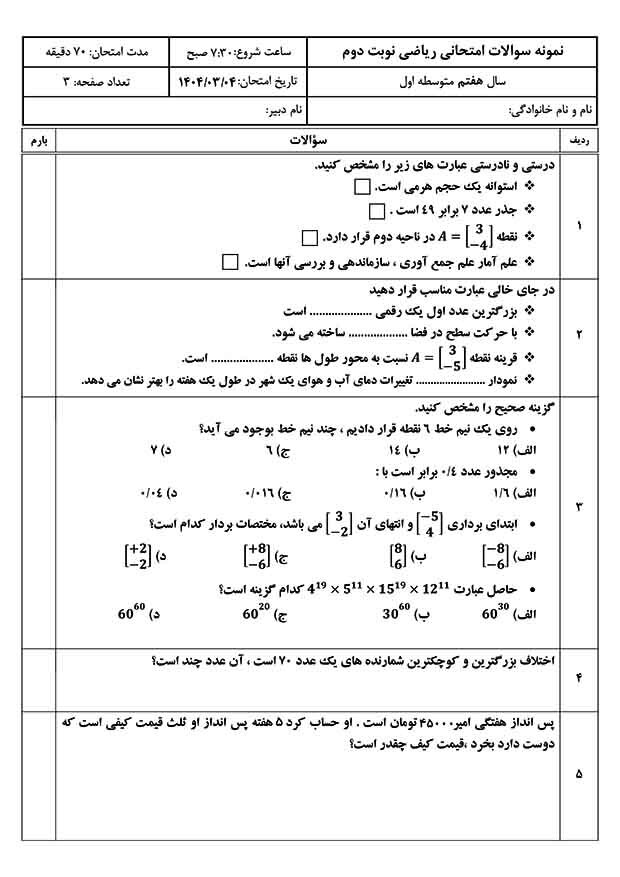
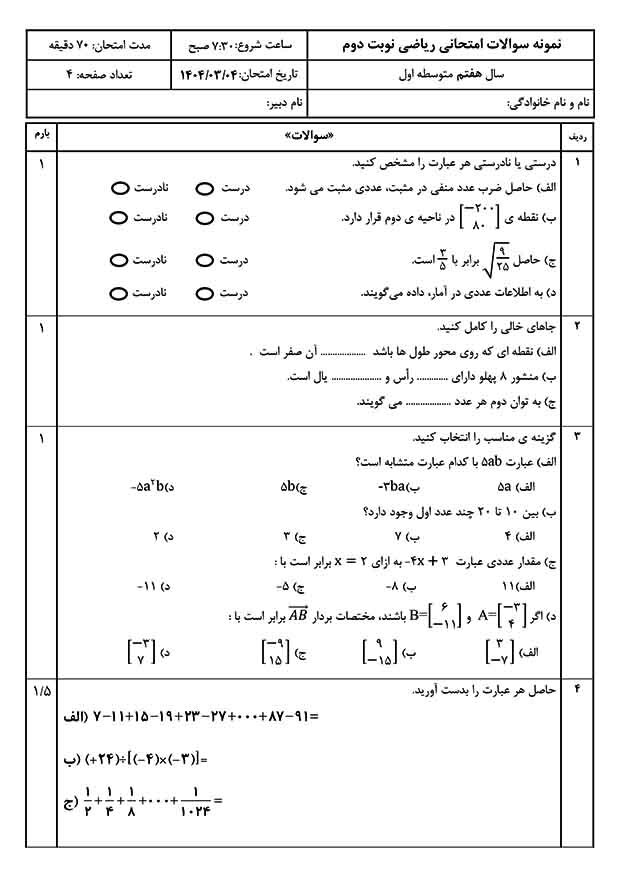
در سدهی هشتم هجری، خاورمیانه و بهویژه ایران با یورشهای ویرانگر تیمور لنگ روبرو بود. اما در آغاز سدهی نهم، نوادهی او، الُغبیگ، حکمرانی علمدوست در سمرقند، زمینهی رشد علمی تازهای را فراهم کرد. یکی از بزرگترین چهرههای این دوران، ریاضیدان و اخترشناس برجسته ایرانی، غیاثالدین جمشید کاشانی بود.
زندگی و آثار)
جمشید بن مسعود بن محمود طبیب کاشانی در شهر کاشان زاده شد و در سال ۸۲۳ هجری قمری (۱۴۳۶ میلادی) در سمرقند درگذشت. او پیش از پیوستن به رصدخانهی سمرقند، کتاب ارزشمند زیج خاقانی را به زبان فارسی تدوین کرد. آثار او شامل مفتاح الحساب، رساله محیطیه، رساله وتر و جیب، و سُلَّمُ السَّماء است.
مفتاح الحساب؛ شاهکار محاسباتی)
کتاب مفتاحالحساب در پنج بخش تنظیم شده:
- حساب اعداد صحیح – شامل چهار عمل اصلی و جذرگیری.
- حساب کسرها – کاشانی نخستین کسی بود که کسرهای دهدهی را وارد محاسبات کرد. او بخش صحیح و کسری عدد را از هم جدا میکرد، مشابه کسرهای شصتگانی که اخترشناسان بابلی استفاده میکردند.
- محاسبات نجومی – با استفاده از دستگاه عددی شصتگانی.
- هندسه و حجمسنجی – شامل مساحت و حجم شکلهای هندسی مانند استوانه، منشور، هرم، کره، گنبد و طاق.
- جبر – بررسی معادلات درجه سوم و چهارم، و ارائهی روشهای هندسی و عددی برای حل آنها.
نزدیکترین مقدار به عدد پی (π) در دوران خودش)
کاشانی در رسالهی محیطیه، مقدار عدد π را با دقتی بیسابقه محاسبه کرد:
π ≈ 3.14159265358979325او این مقدار را از میانگین محیط چندضلعیهای منتظم محاطی و محیطی با ۲ به توان ۲۸ ضلع بهدست آورد:
n = 2^28 = 268,435,456و تصریح کرد که اگر شعاع دایره را برابر فاصلهی زمین تا ستارگان ثابت بگیریم (حدود 600,000 برابر شعاع زمین)، اختلاف بین محیط این دو چندضلعی، از قطر یک موی اسب هم کوچکتر خواهد بود!
محاسبه دقیق سینوس ۳ درجه)
در رسالهی وتر و جیب، کاشانی مقدار sin(3°) را به صورت شصتگانی (مانند ساعت و دقیقه) چنین نوشته است:
sin(3°) = 0° 3′ 8″ 24‴ 33⁗ 59′′′′ 34′′′′′ 28′′′′′′ 14′′′′′′′ 5′′′′′′′′یعنی معادل با:
sin(3°) ≈ 0.0523359562سپس از رابطهی مثلثاتی برای محاسبهی sin(1°) استفاده کرد:
x³ - 3x + a = 0و پاسخ عددی را با دقت بالا بهصورت:
sin(1°) ≈ 0.0174524643783571به دست آورد.
سخن پایانی)
جمشید کاشانی نهتنها یکی از دقیقترین محاسبهگران تاریخ است، بلکه پیشگامی فراموششده در مسیر پیشرفت ریاضی نیز بهشمار میرود. روشهای او، مانند جبر عددی، محاسبهی دقیق عدد پی، حل عملی معادلات درجه سوم و معرفی کسرهای دهدهی، هنوز هم در آموزش ریاضیات جایگاهی شایسته دارند.
منبع: مجله رشد برهان دانش و تفکر ریاضی (دوره متوسطه دوم)، دوره یکم، بهار 1402، شماره 2