محمد بن موسی خوارزمی از برجستهترین چهرههای تاریخ ریاضیات و علوم است؛ دانشمندی ایرانی که در قرن دوم هجری در خوارزم زاده شد و در بغداد دوران شکوفایی علمی خود را گذراند. او در حوزههای گوناگون مانند جبر، حساب، اخترشناسی و جغرافیا آثاری ماندگار به جای گذاشت که برخی از آنها تا سدهها در غرب و شرق جهان تدریس میشدند.
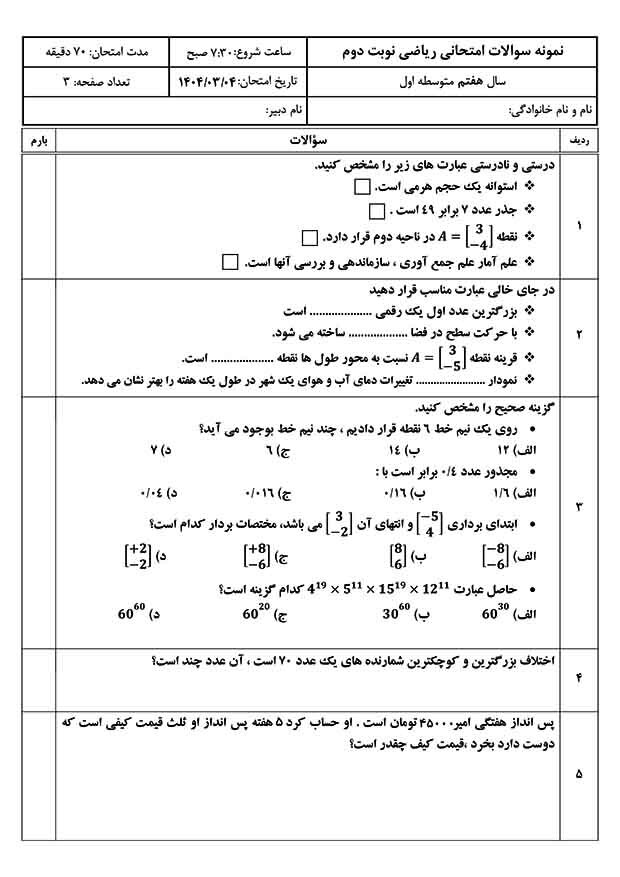
شکلگیری ریاضی به زبان تازه
یکی از مهمترین ویژگیهای کار خوارزمی، تبدیل ریاضیات از حالت هندسی به حالت جبری بود. پیش از او، بسیاری از ریاضیدانان مسائل را بهصورت هندسی و با اشکال حل میکردند؛ اما خوارزمی راهی جدید گشود: توصیف ریاضی به زبان نمادین و توصیفی.
او در کتاب خود با عنوان الجبر و المقابله، بنیان روشی را گذاشت که امروز به عنوان علم جبر شناخته میشود. خوارزمی واژههایی مانند «شَیء» برای مجهول (x)، «مال» برای مربع مجهول (x²) و «جذر» برای ریشه مربع به کار برد.
همچنین دو واژهی معروف «جبر» و «مقابله» که در عنوان کتاب آمدهاند، به ترتیب به معنای انتقال عدد منفی از یک طرف معادله به طرف دیگر (و تبدیل آن به عدد مثبت) و حذف اجزای مشابه در دو طرف معادله هستند.
طبقهبندی دقیق معادلات
خوارزمی معادلههای درجه اول و دوم را در شش دسته طبقهبندی کرد و برای هر دسته، روش خاصی برای حل ارائه داد. این شش نوع معادله به زبان امروزی چنیناند:
- $$x^2 = ax$$
- $$x^2 = a$$
- $$ax = b$$
- $$x^2 + ax = b$$
- $$x^2 + b = ax$$
- $$ax + b = x^2$$
در این دستهبندی، خوارزمی همیشه ضریب \(x^2\) را برابر ۱ در نظر میگیرد و با استفاده از دستورهای توصیفی، مقدار مجهول را به دست میآورد.
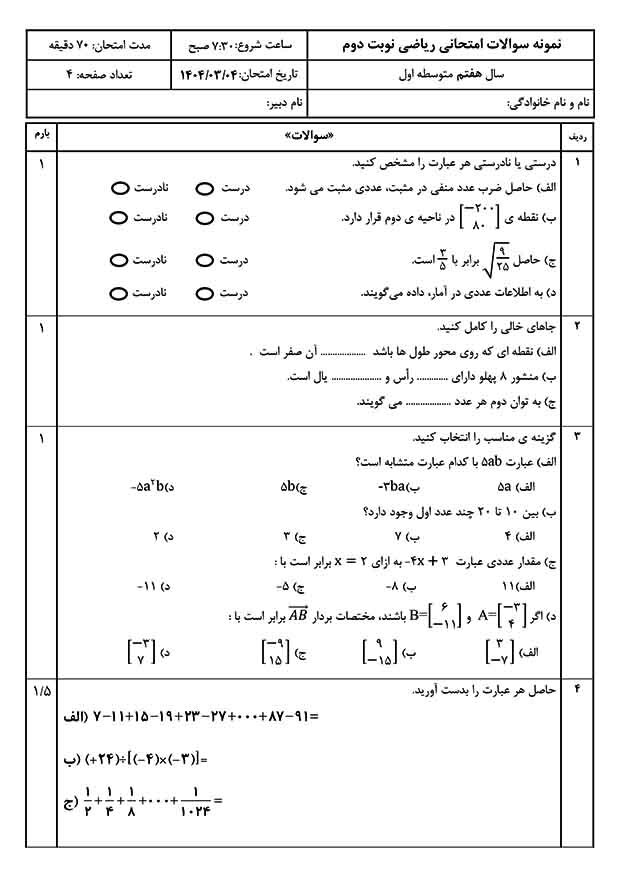
حل هندسی و توصیفی معادلات
از ویژگیهای جالب آثار خوارزمی، بیان همزمان حل جبری و هندسی برای معادلات است. مثلاً برای حل معادلهی:
$$x^2 + 10x = 39$$
ابتدا مربع به ضلع \(x\) رسم میشود، سپس با اضافهکردن مستطیلهایی به ضلعهای آن و تکمیل مربع بزرگتر، مقدار \(x\) به دست میآید.
نمونهای از روش خوارزمی در حل مسئله
یکی از مسائل جالب کتاب جبر او این است:
شخصی یک درهم را بین چند نفر تقسیم میکند. سپس یک نفر به جمع اضافه میشود و درهم دیگری نیز افزوده میشود. این بار، به هر نفر سهمی میرسد که یکششم کمتر از نوبت اول است. تعداد افراد را پیدا کنید.
خوارزمی این مسئله را با روشی توصیفی حل کرده و در نهایت به معادله میرسد:
$$x^2 + x = 6$$
با کاملکردن مربع و یافتن ریشه، مقدار x برابر با 2 به دست میآید؛ یعنی تعداد افراد در نوبت اول دو نفر بودهاند.
واژگان تازه، مفاهیم تازه
خوارزمی پایهگذار زبانی نو برای بیان مفاهیم ریاضی بود. واژهی «الجبرا» که امروزه در زبانهای گوناگون مانند انگلیسی، فرانسوی، روسی و ... رایج است، برگرفته از همان کتاب اوست.
همچنین واژهی «algorithm» ریشه در نام لاتینشدهی «الخوارزمی» دارد که از طریق ترجمهی کتاب حساب او به غرب راه یافت.
تأثیر جهانی
خوارزمی پلی بود میان ریاضیات هندی، یونانی، ایرانی و اسلامی. او با دستهبندی دقیق، مفاهیم پیچیده را سادهسازی کرد و در اختیار نسلهای بعد قرار داد.
در جغرافیا نیز با نگارش صورةالارض، پایهگذار رویکردی تازه در نقشهنگاری شد که از تقسیمات اقلیمی ایران الهام گرفته بود.
سخن پایانی
خوارزمی تنها یک ریاضیدان نبود؛ او معلمی بزرگ بود که زبان تازهای برای بیان علم آفرید. امروز هر جا که معادلهای حل میشود یا الگوریتمی اجرا میشود، نام او زنده است.
منابع:
کتاب «تاریخ ریاضیات» از استاد پرویز شهریاری
مجله رشد برهان ریاضی (دوره متوسطه دوم)، دوره بیست و سوم، بهار 1392، شماره 2