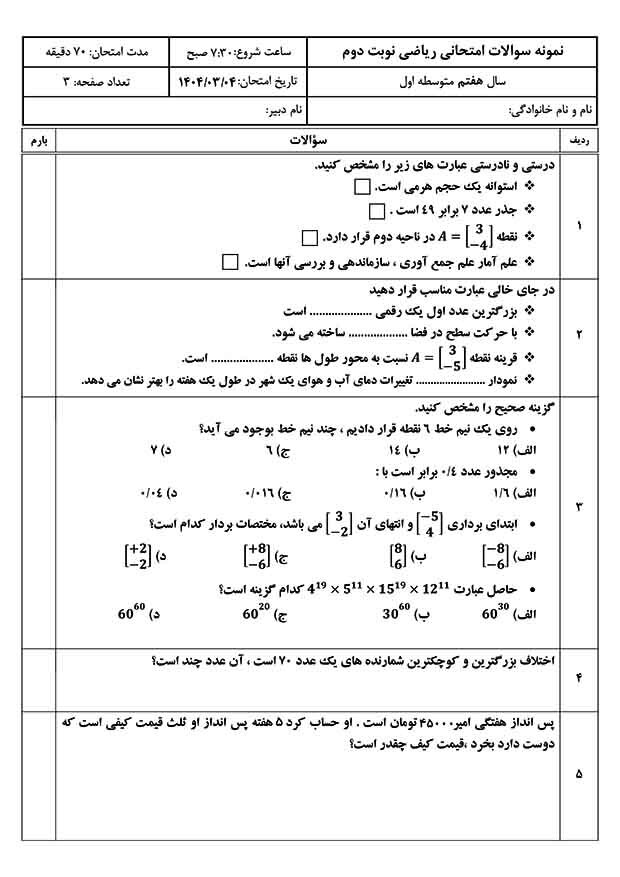
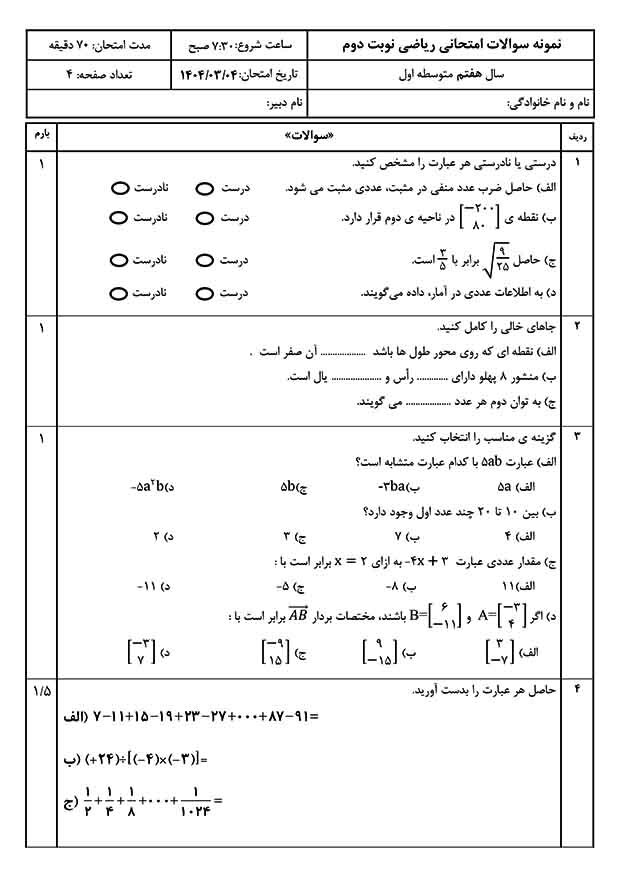
بینظیرترین و سادهترین دستسازه برای معرفی عدد اول، استفاده از الگوی مستطیلی مهرهها است. این دستسازه بصری، درک شهودی و ملموسی از مفهوم عدد اول به دست میدهد.
وسایل مورد نیاز:
مهرههای رنگی (مانند لگو، تیلههای کوچک، دکمه، یا حتی نخود و لوبیا)
یک سطح صاف (مانند میز)
روش اجرا:
یک عدد انتخاب کنید. مثلاً عدد ۶.
از دانشآموز بخواهید با تمام روشهای ممکن، مهرهها را به صورت مستطیلهای منظم (نه خطی) بچیند.
برای عدد ۶ میتوان این مستطیلها را ساخت:یک ردیف ۶ تایی (مستطیل ۱x۶)
دو ردیف ۳ تایی (مستطیل ۲x۳)
حالا یک عدد اول انتخاب کنید. مثلاً عدد ۷.
دوباره از او بخواهید با مهرهها یک مستطیل منظم بسازد. او خواهد دید که تنها یک راه وجود دارد:
یک ردیف ۷ تایی (مستطیل ۱x۷)
نتیجهگیری و معرفی مفهوم:
عدد مرکب: عددی مانند ۶ که میتوان آن را به روشهای بیشتری (غیر از روش خطی) به صورت مستطیل مرتب کرد. یعنی دارای تقسیمکنندههای بیشتری است.
عدد اول: عددی مانند ۷، ۵، ۳ یا ۲ که فقط یک راه برای چیدن آن به صورت مستطیل منظم وجود دارد: یک ردیف به طول خودش. این اعداد را نمیتوان به شکل مستطیلهای واقعی (با بیش از یک ردیف) چید.
جمله کلیدی: عدد اول، عددی است که تنها بتوان آن را به صورت یک «ردیف» چید.
افزودن جذابیت و فعالیت گروهی:
مسابقه سریع: اعداد مختلفی روی کارت بنویسید (مانند ۴، ۵، ۹، ۱۱، ۱۲، ۱۳). بچهها باید با مهرهها برای هر عدد مستطیل بسازند و سریعاً اعلام کنند کدام اعداد اول هستند (آنهایی که فقط یک مستطیل دارند).
استثنای جالب: عدد ۱ فقط یک ردیف ۱ تایی دارد. اما چون فقط یک مقسومعلیه دارد (یعنی خودش)، نه اول است و نه مرکب. این نکته میتواند موضوع یک بحث جذاب در کلاس باشد.
ارتباط با دنیای واقعی:
میتوان اشاره کرد که همین خاصیت اعداد اول (قابل تجزیه نبودن) دلیل اهمیت آنها در رمزنگاری کامپیوترها است. همانطور که نمیتوان یک عدد اول را به مستطیلهای کوچکتر تقسیم کرد، شکستن رمزهایی که بر پایه ضرب اعداد اول بسیار بزرگ ساخته شدهاند نیز برای کامپیوترها فوقالعاده دشوار است. اعداد اول، بلوکهای ساختمانی اعداد طبیعی هستند.
این دستورزی به شکلی مستقیم، ساده و بهیادماندنی، مفهوم پایهای اعداد اول را آموزش میدهد.