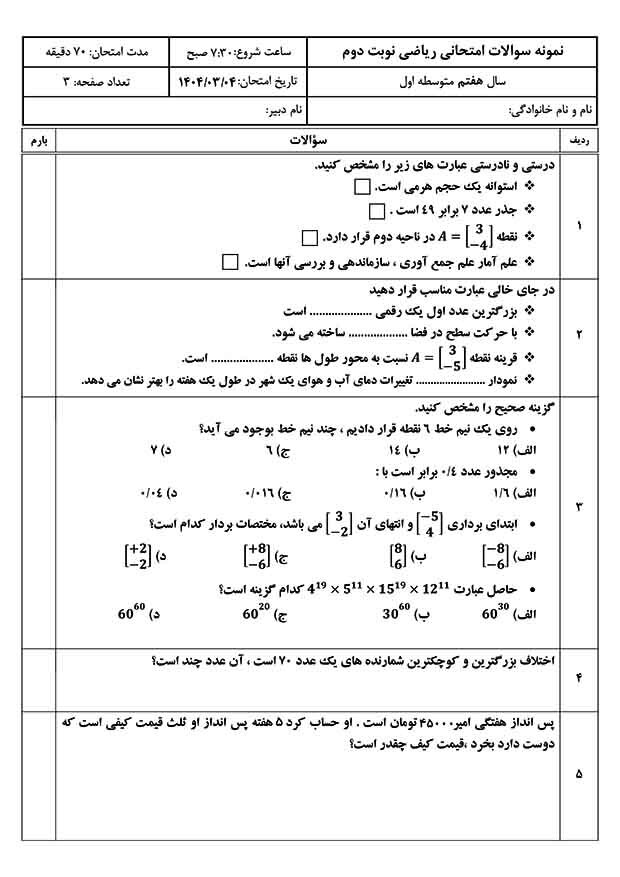
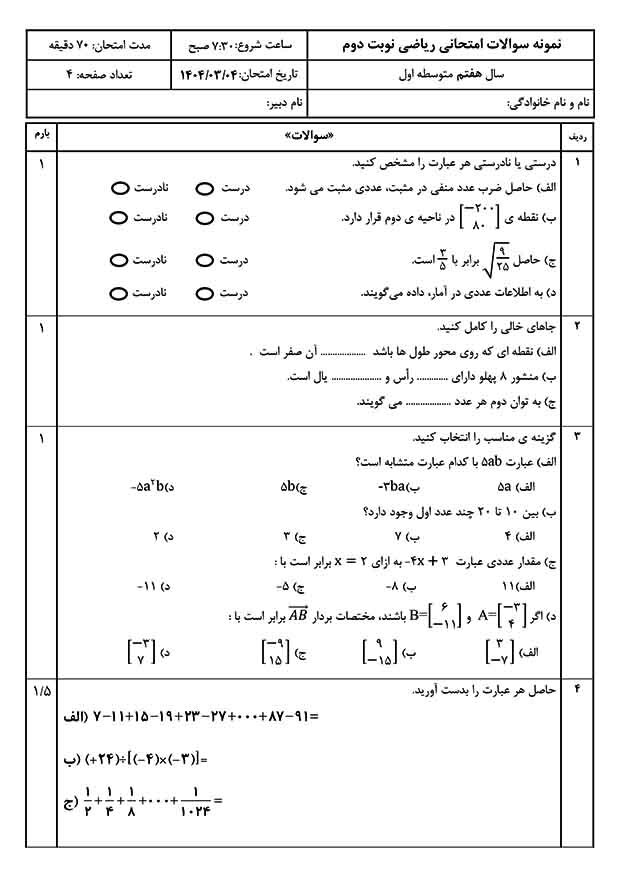
توپ فوتبال از 32 تکه تشکیل شده است: ششضلعیهای سفید و پنجضلعیهای سیاه. هر تکهی سیاه با پنج تکهی سفید احاطه شده است. هر تکهی سفید هم با سه تکهی سیاه و سه تکهی سفید احاطه شده است(شکل زیر). چندتا از تکهها سفيد اند؟

راه حل: به دنبال تکههای سفید هستیم. پس تعداد آن را a در نظر میگیریم. در این صورت، واضح است که تعداد تکههای سیاه برابر است با:
$$ 32 - a $$
اطلاعات داده شده در این مسئله در مورد مجاورت «سیاه» و «سفید» است. پس بهتر است که از دل این اطلاعات، چیزی مانند معادلهای از a بیرون بکشیم. یکی از راههای خوب برای تشکیل دادن معادله، این است که مقداری را برحسب a به دو شیوهی متفاوت، حساب کنیم و با برابر قرار دادن آنها معادلهای به دست بیاوریم.
فرض کنید برای یک ضلع، اسمی مانند «سفیدسیاه» بگذاریم. در واقع، ضلعی را «سفیدسیاه» مینامیم که میان تکهای سفید و تکهای سیاه، مشترک باشد. توجه کنید که هر تکهی سفید (ششضلعی) سه تا ضلع دارد که «سفیدسیاه» هستند و چون تعداد این تکهها برابر با a است، پس تعداد ضلعهای «سفیدسیاه» در کل شکل، برابر است با:
$$ 3a $$
از طرف دیگر، هر تکهی سیاه (پنجضلعی) پنج تا ضلع «سفیدسیاه» دارد و با توجه به تعداد تکههای سیاه، میتوان گفت که تعداد ضلعهای «سفیدسیاه» در کل شکل برابر است با:
$$ 5(32 - a) $$
چون این دو مقدار با هم برابرند، پس:
$$ 5(32 - a) = 3a $$
با حل این معادله، معلوم میشود که تعداد تکههای سفید برابر است با 20.
منبع: کتاب «هندسه از ابتدا تا ...» از ارشک حمیدی، انتشارات فاطمی