یک مثال جالب از کسرهای تلسکوپی

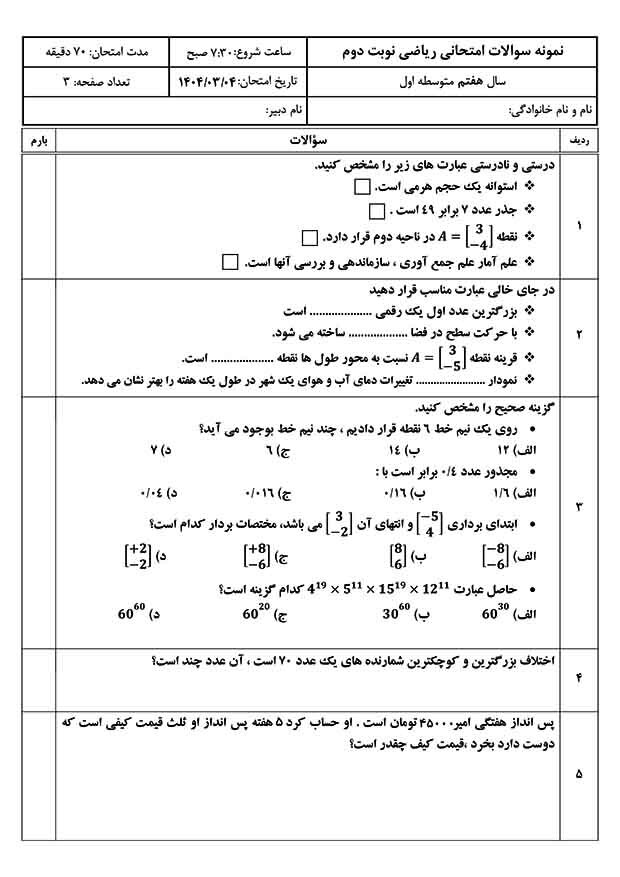
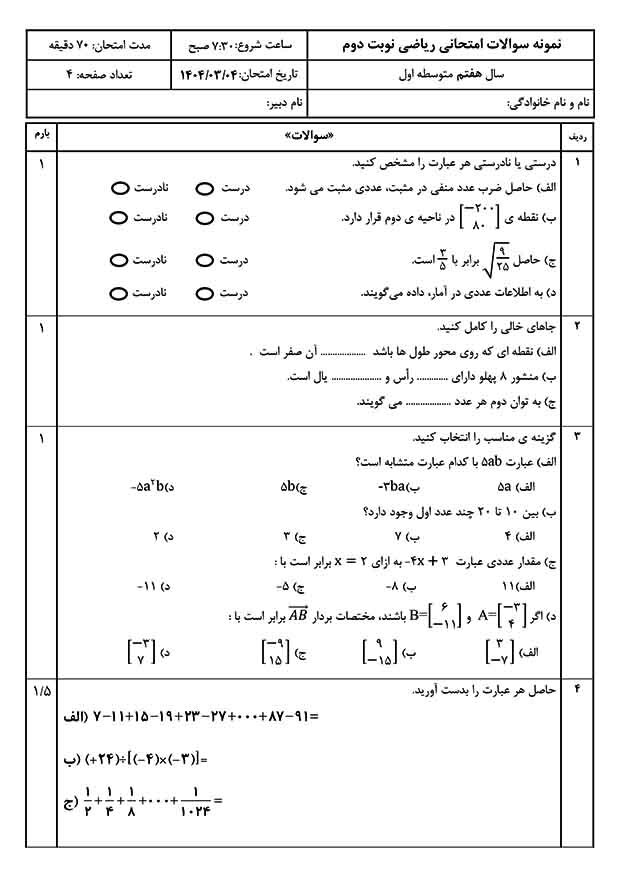
توجه: اگر از موبایل برای خواندن این مقاله استفاده می‌کنید، موبایل خود را به صورت افقی در دست گرفته و صفحه را از نو باز کنید.

در این مثال می‌خواهیم مجموع زیر را محاسبه کنیم:

$$\frac{3}{1}+\frac{3}{1+2}+\frac{3}{1+2+3}+...+\frac{3}{1+2+3+...+100}=?$$

ابتدا عدد ۳ را از تمام جملات فاکتور می‌گیریم:

$$=3\left(\frac{1}{1}+\frac{1}{1+2}+\frac{1}{1+2+3}+...+\frac{1}{1+2+3+...+100}\right)$$

مرحله ۱: تبدیل مجموع عددی به فرمول بسته)

می‌دانیم که مجموع عددهای طبیعی از ۱ تا n برابر است با:

$$1+2+3+...+n=\frac{n(n+1)}{2}$$

پس هر مخرج را با استفاده از این فرمول جایگزین می‌کنیم.

$$=3\left(\frac{1}{\frac{1\times2}{2}}+\frac{1}{\frac{2\times3}{2}}+\frac{1}{\frac{3\times4}{2}}+...+\frac{1}{\frac{100\times101}{2}}\right)$$

مرحله ۲: ساده‌سازی مخرج‌ها)

در هر کسر، ضرب در دو باعث حذف عدد ۲ در مخرج می‌شود:

$$=3\left(\frac{2}{1\times2}+\frac{2}{2\times3}+\frac{2}{3\times4}+...+\frac{2}{100\times101}\right)$$

سپس ۲ را هم از پرانتز بیرون می‌آوریم تا محاسبه راحت‌تر شود:

$$=6\left(\frac{1}{2}+\frac{1}{2\times3}+\frac{1}{3\times4}+...+\frac{1}{100\times101}\right)$$

مرحله ۳: بازنویسی به فرم تلسکوپی)

هر جمله از این نوع را می‌توان به شکل تفاضلی نوشت:

$$\frac{1}{n(n+1)}=\frac{1}{n}-\frac{1}{n+1}$$

با جایگذاری این فرمول در عبارت بالا، به مجموعه‌ای از جمله‌هایی می‌رسیم که در هم حذف می‌شوند:

$$=6\left(\frac{1}{2}+(\frac{1}{2}-\frac{1}{3})+(\frac{1}{3}-\frac{1}{4})+...+(\frac{1}{100}-\frac{1}{101})\right)$$

مرحله ۴: حذف جملات میانی)

$$=6\left(\frac{1}{2}+\frac{1}{2}-\frac{1}{101}\right)$$

نتیجه نهایی)

حالا کافی است حساب کنیم:

$$=\frac{600}{101}$$

این مثال نشان می‌دهد که چگونه با استفاده از ویژگی کسرهای تلسکوپی می‌توان مجموع‌های ظاهراً پیچیده را به روشی ساده و زیبا محاسبه کرد.